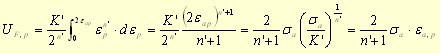Feltner method

The Feltner method is based on relating the energy spent on loading to the maximum load with the parameters of the e-N curve (see also the picture below). Feltner describes the plastic part of the energy by the half of hysteresis loop:

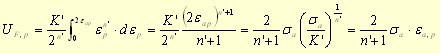where the form of parameters before the integral was set by a fit to results. The energy is not the same as a half of the Morrow parameter as it should be - it lacks the coeffiecient (1-n'). The complete parameter of Feltner is:

The exponent n' of the Ramberg-Osgood curve is replaced by the ratio of b and c exponents (see e-N curve) - beware that if you set it value directly in PragTic, the ratio of those two exponents b and c will be still used instead. The stress and plastic strain amplitudes are related to Basquin and Manson-Coffin curves:

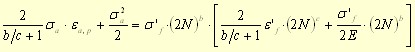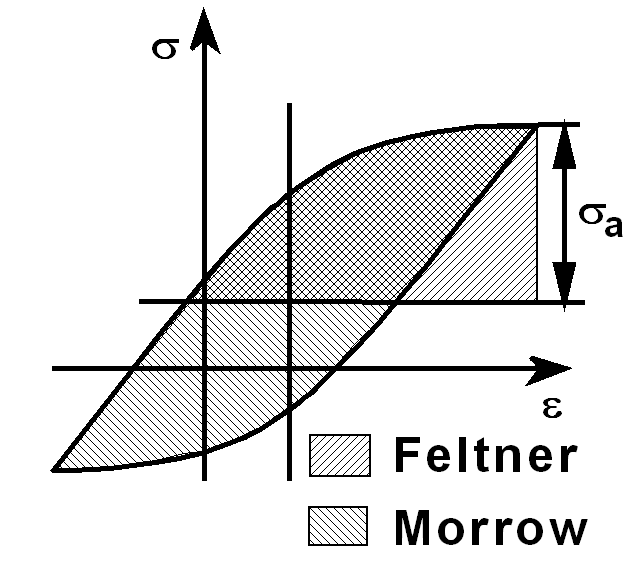
Fig.: Feltner method analysis is based on the energy applied during loading, while the Morrow parameter is related to the energy closed in the hysteresis loop.

The Feltner criterion in the original form lacks any adjustment to mean stress effect. The SWT correction for computation of the equivalent stress is therefore applied to all stress amplitudes in the previous formula:

Negative mean stress is expected to be non-damaging and its value is reset to zero. The conversion to an equivalent value allows a use of the common uniaxial rain-flow decomposition. The choice of the appropriate decomposition method is the point in Calculation Methods window, where the way of the tensor's reduction is chosen.

Mark	Unit	PragTic variable	Meaning
	[MPa]		stress amplitude
	[MPa]		mean stress
	[-]		strain amplitude
	[-]		plastic strain amplitude
E	[MPa]	E	tensile modulus
	[MPa]	SIG_F	fatigue strength coefficient
	[-]	EPS_F	fatigue ductility coefficient
b	[-]	EXP_B	fatigue strength exponent
c	[-]	EXP_C	fatigue ductility exponent
K'	[MPa]		cyclic hardening coefficient
n'	[-]		cyclic hardening exponent
N	[-]		number of cycles to crack initiation

E	[MPa]	tensile modulus
NU	[-]	Poisson’s ratio
SIG_F	[MPa]	fatigue strength coefficient
EPS_F	[-]	fatigue ductility coefficient
EXP_B	[-]	fatigue strength exponent
EXP_C	[-]	fatigue ductility exponent